目录
快速导航-
教学纵横 | 大单元视角下恒成立复习课的教学探索 南京航空航天苏州附属(215000)
教学纵横 | 大单元视角下恒成立复习课的教学探索 南京航空航天苏州附属(215000)
-

教学纵横 | 促进数学思维自然生长的问题驱动教学研究
教学纵横 | 促进数学思维自然生长的问题驱动教学研究
-

教学纵横 | 教学设计应把握学生自主学习的课堂主体
教学纵横 | 教学设计应把握学生自主学习的课堂主体
-

教学纵横 | 高中数学情景教学法的“内涵美”
教学纵横 | 高中数学情景教学法的“内涵美”
-

教例探微 | 意外与美好相伴 反思与进步相随
教例探微 | 意外与美好相伴 反思与进步相随
-

教例探微 | 理解运算本质,破解解几中的共弦问题
教例探微 | 理解运算本质,破解解几中的共弦问题
-
教例探微 | 立足本质 揭示内涵 提升素养
教例探微 | 立足本质 揭示内涵 提升素养
-
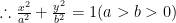
聚焦高考 | 2024年全国甲卷理科第20题的多解与推广 浙江省诸暨中学 (311800)
聚焦高考 | 2024年全国甲卷理科第20题的多解与推广 浙江省诸暨中学 (311800)
-
聚焦高考 | 一题多解扩思路,透过现象巧证明
聚焦高考 | 一题多解扩思路,透过现象巧证明
-

聚焦高考 | 借助一题多解 发展核心素养
聚焦高考 | 借助一题多解 发展核心素养
-

聚焦高考 | 破解一道以矩阵范数为背景的创新压轴题 福建省龙海第二中学 (363199)
聚焦高考 | 破解一道以矩阵范数为背景的创新压轴题 福建省龙海第二中学 (363199)
-

聚焦高考 | 一题多解提升思维 一题多变发展素养
聚焦高考 | 一题多解提升思维 一题多变发展素养
-

初数研究 | 数学通报问题2816号的证明与拓展
初数研究 | 数学通报问题2816号的证明与拓展
-
初数研究 | 用二次函数的一个性质证明一类无理不等式
初数研究 | 用二次函数的一个性质证明一类无理不等式
-
初数研究 | 拿破仑定理的证明及其应用探究
初数研究 | 拿破仑定理的证明及其应用探究
-
初数研究 | 一道椭圆中内接三角形面积最值问题的探究
初数研究 | 一道椭圆中内接三角形面积最值问题的探究
-

解题方法与技巧 | 基于波利亚解题表处理情境问题的探究
解题方法与技巧 | 基于波利亚解题表处理情境问题的探究
-

解题方法与技巧 | 一道不等式恒成立求参数试题的解法探析
解题方法与技巧 | 一道不等式恒成立求参数试题的解法探析
-

解题方法与技巧 | 一道解三角形问题的多角度探究
解题方法与技巧 | 一道解三角形问题的多角度探究
-

解题方法与技巧 | 解题未动 思想先行
解题方法与技巧 | 解题未动 思想先行
-
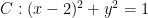
解题方法与技巧 | 一道抛物线内三角切圆问题的求解探究
解题方法与技巧 | 一道抛物线内三角切圆问题的求解探究
-

解题方法与技巧 | 一道解析几何题的巧解及推广
解题方法与技巧 | 一道解析几何题的巧解及推广
-
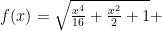
竞赛之窗 | 观察式子结构特征,巧解几类竞赛试题
竞赛之窗 | 观察式子结构特征,巧解几类竞赛试题
-
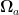
竞赛之窗 | 例析几道数学竞赛中动球和多球问题的解法
竞赛之窗 | 例析几道数学竞赛中动球和多球问题的解法
-

竞赛之窗 | 一个不定方程模型在强基、竞赛中的变形考查
竞赛之窗 | 一个不定方程模型在强基、竞赛中的变形考查




















 登录
登录